This is a nice problem from the book “Cut the knot”, which is a compilation of probability riddles and brain teasers. I like the book because many of the problems are about intuitive reasoning, and don’t really involve that much technical knowledge of probability theory, so they can be fun to do with people who don’t have a formal maths background. Each problem can also generally be solved many different ways, so it’s fun to compare solutions.
Problem
Two numbers \( X \) and \( Y \) are randomly chosen from the interval \( [0, 1] \). Let \( r \) denote the quotient of the larger of the two by the smaller: \( r = \frac{\max(X,Y)}{\min(X,Y)} \). Depending on the assumptions, there are three questions. For a given \( k > 0 \), what is the probability that \( r ≥ k \)
- if \( X \) is uniformly distributed on \( [0, 1] \) and \( Y \) is uniformly distributed on \( [X, 1] \)?
- if \( X \), \( Y \) are jointly uniformly distributed on \( \\{(x, y) : 0 ≤ x ≤ y ≤ 1\\} \)?
- if \( X \) and \( Y \) are uniformly and independently distributed on [0, 1]?
Source: Cut the knot by Bogomolny, Ex. 7.6
Solution
We’re given that \( X\sim U(0, 1) \) and that \( Y|X\sim U(X, 1) \), this implies that the variables have the densities \begin{align} p(x)&=1 \quad \forall \quad x\in[0, 1] \\\ p(y|x)&=\frac{1}{1-x} \quad \forall \quad y\in[x, 1] \end{align} which implies that the variables have the joint density given by
$$ p(x, y) = p(x)p(y|x)= \frac{1}{1-x}. $$Now let’s have a think about how to compute the require probability \( \mathbb{P}(r\geq k) \). First, it is clear that in this case \( Y\geq X \), so \( r\geq1 \) which implies \( \mathbb{P}(r\geq k)=1 \) when \( k<1 \). The fact that \( Y\geq X \) also implies that \( r = \frac{\max(X,Y)}{\min(X,Y)}=\frac{Y}{X} \). The key thing to realize here is that we can equivalently write \( \mathbb{P}(r\geq k) \) as \( \mathbb{P}(\frac{Y}{X}\geq k)=\mathbb{P}(Y\geq kX) \).
We actually now have all the parts we need to solve the question, but realizing this is a little easier with a picture. The diagram below shows all the information we have. The variables \( x \) and \( y \) are shown on each axis, with the shaded region showing the probability density of different \( (x,y) \) pairs. Notice that the lower triangle is unshaded since we know \( y>x \). Also plotted on the diagram is the line \( y=kx \).
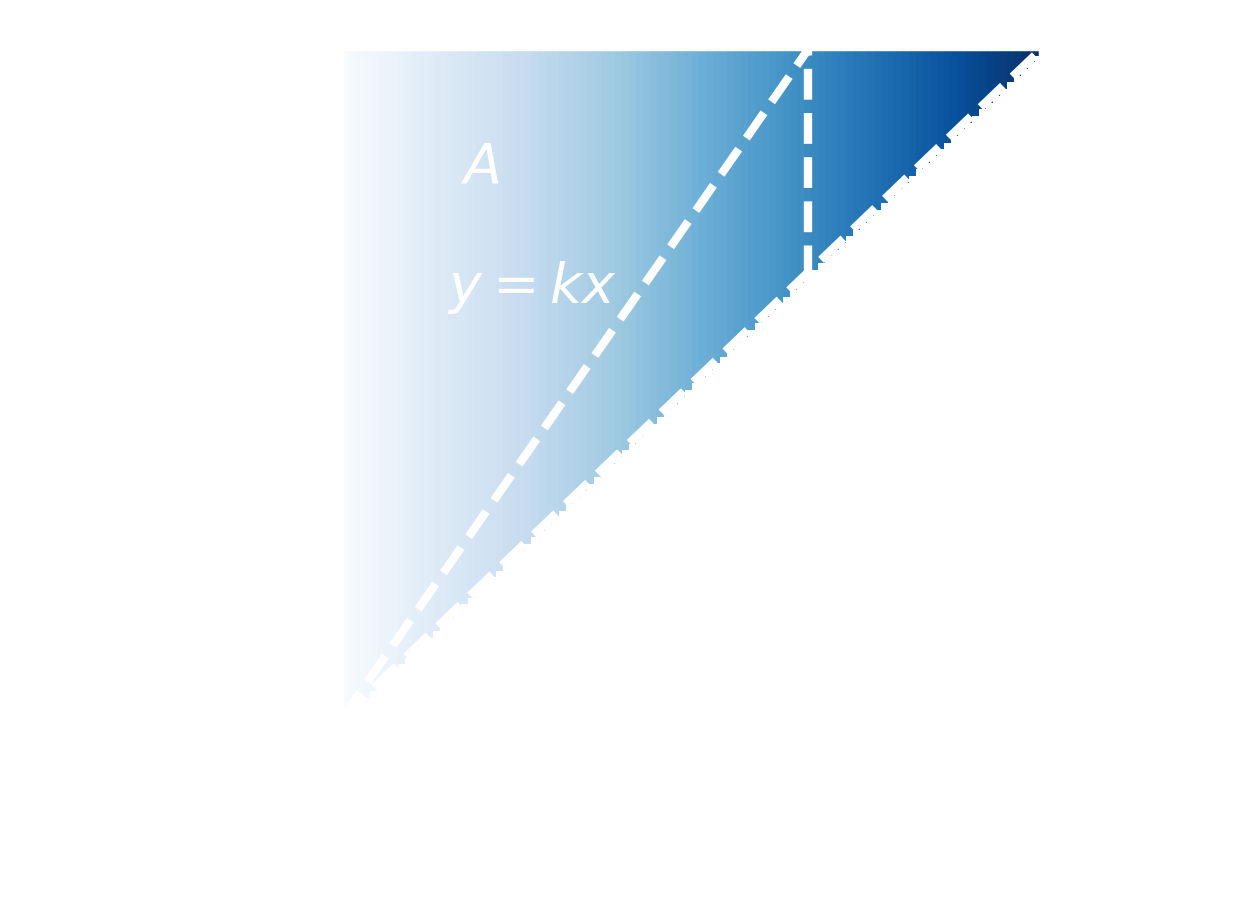
All our information.
What we want to know is the probability that \( (x,y) \) lies in the region \( A \), i.e the region bounded by \( 0\leq y \leq 1, y\geq kx \). To do this we need to integrate the joint density over this region. This probability is given by \begin{align} \mathbb{P}(r\geq k) &= \int^{1/k}_{0} \int^{1}_{kx}p(x,y)dydx\\\ &= \int^{1/k}_{0} \int^{1}_{kx} \frac{1}{1-x}dydx \\\ &= \int^{1/k}_{0} \frac{1-kx}{1-x}dx \\\ &= 1 + (k-1)\log\left(\frac{k-1}{k}\right) \end{align} Part 1 solved!
Now we have this setup the answers for the next two parts are actually quite simple. For part 2, we have the exact same setup, only now we are given that the \( X,Y \) are jointly uniform over the region \( 0\leq x\leq y \leq 1 \). The diagram would look exactly the same, but with the shading being uniform over the region. The joint density is now \( p(x,y)=2 \) (since the area of the region is \( 1/2 \)), so \begin{align} \mathbb{P}(r\geq k) &= \int^{1/k}_{0} \int^{1}_{kx}p(x,y)dydx\\\ &= 2\int^{1/k}_{0} \int^{1}_{kx} dydx \\\ &= \frac{1}{k} \end{align}
Now for the final part, we can use the symmetry of the problem to get the answer easily. When \( Y>X \) we have the same setup as above, and when \( X>Y \) we have the region \( 0\leq x\leq 1, y\leq\frac{x}{k} \), which is the mirror image of the region from part 2, reflected in \( y=x \). We sum these regions to get the answer. Not that the density is now \( p(x,y)=1 \), so we get that
$$ \mathbb{P}(r\geq k) = \frac{1}{2k} + \frac{1}{2k} = \frac{1}{k} $$